Understanding cognitive skills and math.
“Math!” This four-letter word is enough to give many kids a knot in the stomach, and many parents sleepless nights in anticipation of the next school report or math test coming up.
When it comes to mathematics, many parents and children feel anxious and frustrated. This is especially true when a child is struggling with math, in spite of already getting help by means of tutoring, extra math classes or math programs.
For many parents, and similar for their children, their math anxiety began with timed math tests in primary school. They knew the answers, but their brains froze when up when working against the clock. For others, not understanding the why behind a math formula was confusing.
Unfortunately, children who experience math anxiety often grow up without ever understanding the reason for their math struggles and carry math anxiety with them for the rest of their lives. As a parent, they feel helpless when their child brings home math homework.
Some may become teachers who feel powerless when their students don’t understand math or label themselves as not being a math person. Their math anxiety and frustration gets passed on to the children, and the cycle unfortunately continues.
Math anxiety is very real, are extremely debilitating, and have been studied for decades. Yet it persists.
But why is math so difficult for some kids?!
The answer to this question usually lies within the strengths and weaknesses in our individual cognitive profiles. Each of us have strong and weaker cognitive skills – those underlying brain skills essential for learning, reading, reasoning, attention, and yes – math.
And when it comes to math (and learning), having strong cognitive skills is a prerequisite for learning math.
If one or a combination of skills like selective, sustained and divided attention; visual processing; visual, sequential and working memory; long term memory, deductive and inductive reasoning are weak, they must be strengthened first, before a child will be able to understand and apply math.
So let’s explore the connection between cognitive skills and math.
As the foundation for learning, cognitive skills are essential across any curriculum, including math
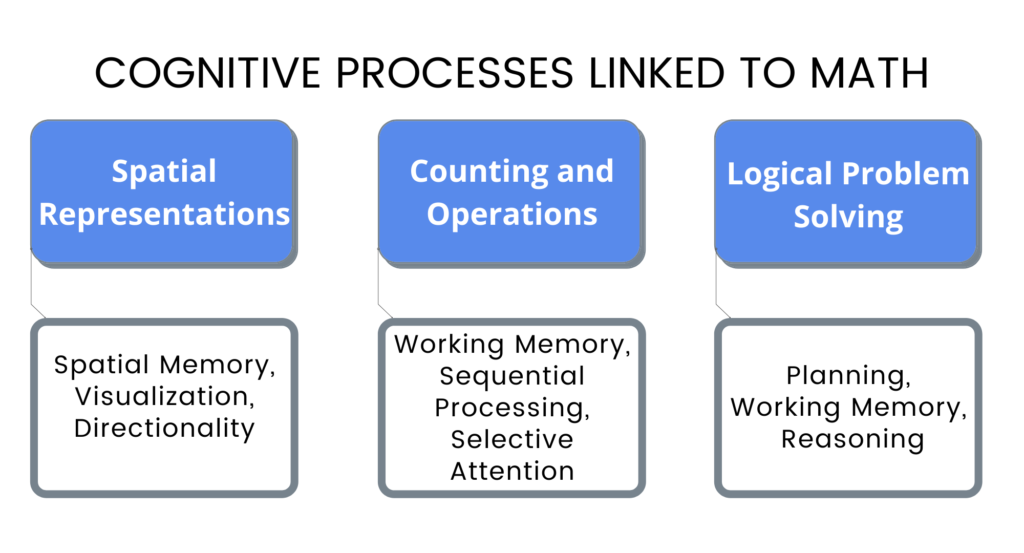
What, then, are the important underlying cognitive processes that support or impair our learning of math? According to scientific and educational researchers, math skills can be grouped into the following categories:
SPATIAL REPRESENTATION
The relationship of math success to visual-spatial abilities is strongly supported by research, and the correlation appears to increase as the complexity of the math task increases.
The important aspect of visual-spatial processing is not just remembering the shape, size, colour and number of objects, but their relationship to each other in space. It turns out that visual memory by itself (what things are) is somewhat error-prone, but spatial memory (where things are) is associated with correct answers, and is thus an important aspect of mathematical problem solving.
Within visual-spatial processing, we can distinguish cognitive skills such as the following:
- Spatial Memory: This refers to our ability to remember where we are in space and where we are related to other objects in space. This understanding provides the foundation on which problems (changes in the space) can be solved.
- Visualization: Our ability to visualize a problem we need to solve or to visualize alternative solutions contributes substantially to our understanding of the problem. When we learn transformations in geometry, for example, interpreting the difference between a translation (sliding an object along a straight line), a rotation (turning an object around a point) and a reflection (mirror image) is greatly aided by our visualization skills.
- Directionality: The ability to distinguish between left and right, of course, is more than just about math. It comes in handy when tying shoe laces, reading a map, and in playing sport. Here’s an example of how we use directionality – imagine someone hands you a map with a route marked out on it. Do you have to keep turning the map around to figure out what direction to turn next? If so, your directionality skills are not as strong as they might be.
COUNTING AND OPERATIONS
When it comes to counting and numerical operations, we are again dependent for math success on some foundational cognitive skills, such as sequential processing and selective attention, and on executive functions (the directive capacities of our minds) such as Working Memory:
- Working Memory: Working Memory is to our ability to hold information in our minds while we manipulate it. Working memory capacity is highly correlated with reading comprehension, with math performance, and with many other academic and non-academic outcomes. Working Memory serves math processes from the very simple (for example, keeping track of which oranges in the basket we’ve counted and which we haven’t) to the most complex reasoning and mental simulations we perform when calculating statistics or contemplating string theory or manipulating derivatives in calculus.
- Sequential Processing: Counting is all about sequences, so once again, cognitive skills contribute crucially at even the most elementary stages of math. As we start to manipulate and calculate, the sequence of steps to solve a problem must be observed. A concrete example is the concept of order of operations and the different result that comes from (7 + 4) x 3 and from 7 + (4 x 3).
- Selective Attention: When we have good selective attention skills, it’s easier for us to screen out the irrelevant parts of a complex problem and isolate the relevant facts that we need to concentrate on. For example – if Susan, who is wearing a red dress, is 2 years older than Ben, who is wearing a blue shirt and jeans and just celebrated his 12th birthday, we don’t need to know the colour of their clothes to determine how hold Susan is.
LOGICAL PROBLEM SOLVING
Undoubtedly, math is problem-solving. There are of course other types of problem-solving, but problems with numbers almost always call for mathematical thinking and logic to be applied.
Above, we have already highlighted some of the cognitive skills we use for problem-solving, but higher-order cognitive processes are often required to be successful in math. These include:
- Planning: Here’s a simple example of how we use Planning, one that might sound familiar: I’m in school and learning long division. I’m supposed to ‘write down my answer and include a specific number of decimal places. I write the problem on my paper and then, halfway through, I realize that I wrote the problem too far to the right side of my page. That was a lack of planning. Good planning on the other hand, is when we consider alternative approaches to a problem, map out the sequence of steps in advance, and then carry them out efficiently and accurately.
- Working Memory: Let’s look at an example of a child who’s always struggling to finish her math class work and homework. She might understand the core concepts of what she has to do, but she has limited Working Memory capacity. When she has to copy a problem from her math book onto her homework book (let’s say 267 x 3), she would have to copy each number by itself, first the 2, then the 6, and so on. She cannot remember 267, much less the entire math problem. Working Memory is essential to hold the elements of any math problem in mind, consider different approaches, and keep track of where we are in a sequence of steps to solve a multi-step math problem.
- Logic and Reasoning: Undoubtedly math is logical and will put demands on our reasoning skills. As we learn about math theories or explain how we draw conclusions, we have to recognize patterns, analyze cause and effect, test hypotheses and determine whether to include or exclude items from sets. For all of these, we rely heavily on our logic and reasoning ability.
As we acknowledge how critical cognitive skills are to math and learning, it raises the question of how we can support our children in developing these skills so that they can be effective learners.
In the next article, we will look at how cognitive skills can be strengthened and share tips and exercises parents can use at home.
- Why is math so difficult for some kids? - September 14, 2023






1 thought on “Why is math so difficult for some kids?”
Maths is so difficult because it has plenty of multi-step processes to solve problems and in order to master it, one need to practice a lot but many students and learners are lazy to practice.